浮点数准确性问题
背景
用户有时候会遇见浮点数计算或者筛选预览得到的结果和预想的不太一样,绝大多数都和浮点数的精度有关系。基于二进制的存储方式使得浮点数本身存在一定的精度问题,而多次计算后的浮点数,精度问题会更加明显。下面,来介绍一下关于浮点数精度的处理。
测试
数据抽取
在csv文件中创建以下数据:
col6,col7,col12,col6_2,col7_2,col12_2
0.999999,0.9999999,0.999999999999,0.999999,0.9999999,0.999999999999
1.000001,1.0000001,1.000000000001,1.000001,1.0000001,1.000000000001
我们把csv上传到观远BI中,前三列选择为DOUBLE类型,后三列选择为STRING类型,在BI中预览数据可以看到实际显示的结果如下:

数据集中的浮点数如果为0.999999(col6),在前端预览后得到的结果也会是0.999999。但是如果数据集的浮点数为0.9999999(col7, 小数点后7位),那预览得到的结果是1。
原因:在观远BI系统中,浮点数是存在显示精度的,默认的浮点数精度为小数点后6位,小数点后第7位就是误差位。而Spark底层存储的数据是精度更高的数据(参考STRING类型),计算和筛选都是基于底层存储的数据来进行的。
数据计算
基于上面的数据集,做一个ETL,仅保留要用的字段col7和col7_2,用col7减去0.5,再乘以0.1,再用round来取近似值。round会根据截断的后一位做4舍5入, 保留指定小数位数。
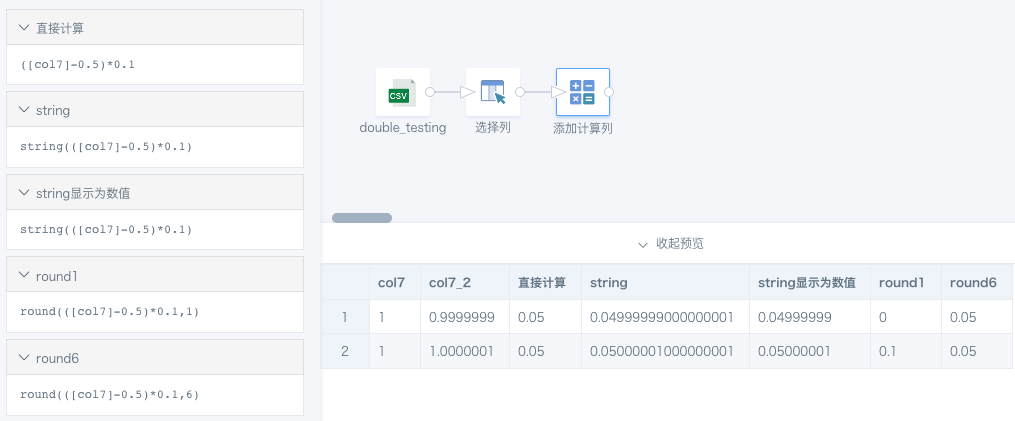
我们可以看到两组数据在直接计算后得到都是0.05,但是做round(1)的时候,得到的结果是不一样的。根据col7_2原始数据计算,我们设想得到计算结果应该是「string显示为数值」的这列,但是实际上在spark中存储的数据应该是「string」的数据,会有十几位小数(double小数部分能精确到小数点后的15位),最后一位是计算产生的误差数。
数据筛选
创建一个包含数值0.000000000000000000001(小数点后有21位)的数据集,或者在BI中新建一个数值类型字段,预览都显示为0;把该数值转换为文本STRING, 显示为科学计数法。以下图为例,筛选 col21 >0 是可以筛选出这条数据的。
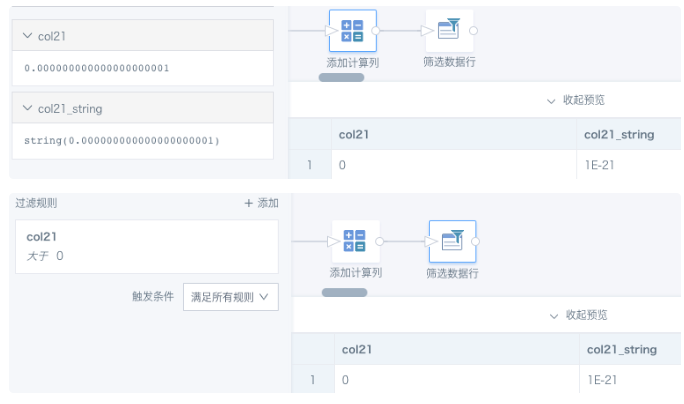
从以上的2个实验可以得出结论:对double类型浮点数计算,数据精度会发生变化、产生误差,但是做筛选比较的时候,即使是20位以上的小数依旧能被识别出来。所以,我们计算产生的误差会让浮点数筛选结果不准确。
解决方案
先通过round(x)取到我们想要的精度的数,然后再做筛选。精度的选取,一般可以选取round(6),这个和BI的默认显示精度是一样的。如果知道自己数据本身的精度,也可以采用数据原精度,也可以把字段转换为精度更高的demical类型。例如 cast([数值] as decimal(15,6)) , 15代表最多15个数字,其中有6位小数。
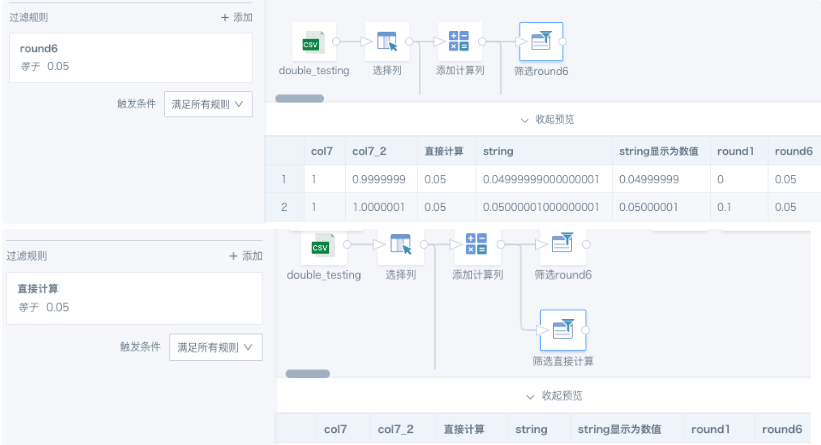
上面第一个案例,如果不用round函数对数值做近似值,想要筛选出col7计算出的0.05,是筛选不出结果的。两种筛选结果对比参考下图。
FAQ
整数用函数转换为文本后为什么带小数点?
原因:在BI里新建计算字段,选“数值”类型或者对字段值进行数学计算,输出类型默认为double,系统对数据四舍五入,保留6位小数后,对尾部的0自动抹除。例如四舍五入后数据为1.0,那么显示为1;数据为0.100000,则显示为0.1。
解决方案:需要一直保持为整数的话,需要用函数转换为整数,例如 int()/cast( as int).
四舍五入结果为什么不对?
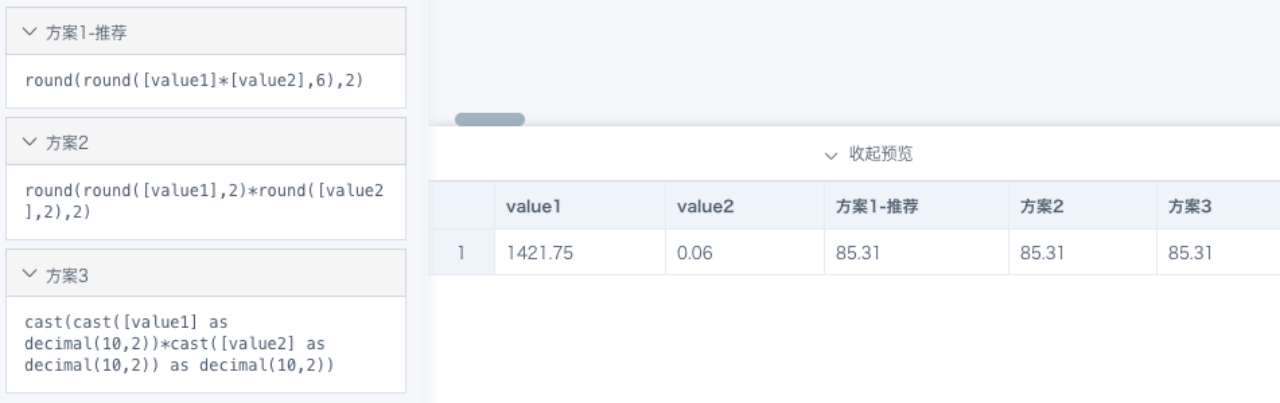
案例:例如 1421.75*0.06=85.305,四舍五入保留2位小数应该是85.31,但是round(2)后是85.3。
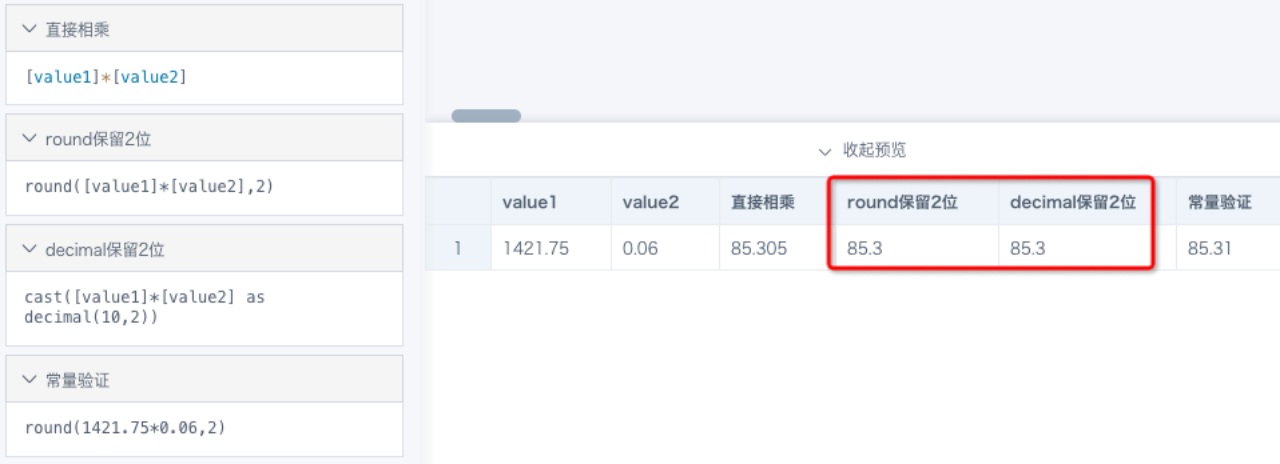
原因:从BI里看到的1421.75和0.06两个值已经是四舍五入后的结果,并不代表原始准确数据,85.305是对计算结果四舍五入,保留6位小数的结果, 相当于 round(6), 和 round(2)精度不同,不能保证结果相等。
解决方案:round(2)后等于85.3也是合理的计算结果;如果需要按照85.305继续四舍五入,建议使用 round(round([数值1]*[数值2],6),2)。实现方案可能有多种,建议根据实际情况灵活运用(参考下图)。
筛选数值>0后,为什么计数结果变来变去不准确?
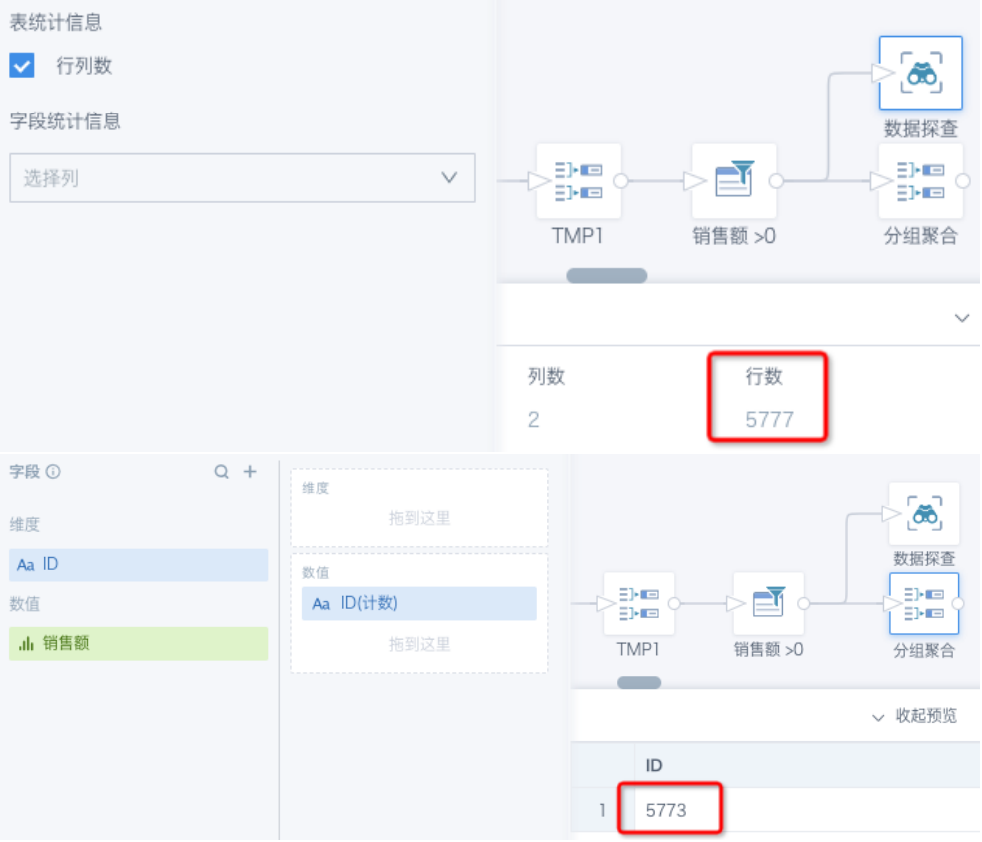
原因:每一次新的查询,前面数据要重新计算并筛选,每次数据的精度可能会有肉眼不可见的变化,那么筛选结果就可能产生误差。
解决方案:指定数值精度后再对比。例如改为筛选 [销售额]>0.000001,或者 round([销售额],6)>0, round([销售额],6)>0.000001。